Planar graph

Example graphs
Planar Nonplanar
Butterfly graph.svg
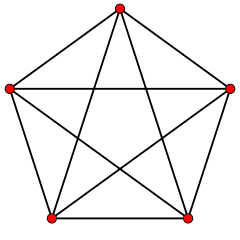Butterfly graph		 Complete graph K5.svg
K5
CGK4PLN.svg
The complete graph
K4 is planar		 Biclique K 3 3.svg
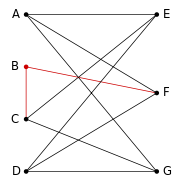
K3,3

In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints.

A planar graph already drawn in the plane without edge intersections is called a plane graph or planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point in 2D space, and from every edge to a plane curve, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points. Plane graphs can be encoded by combinatorial maps.

It is easily seen that a graph that can be drawn on the plane can be drawn on the sphere as well, and vice versa.

The equivalence class of topologically equivalent drawings on the sphere is called a planar map. Although a plane graph has an external or unbounded face, none of the faces of a planar map have a particular status.

A generalization of planar graphs are graphs which can be drawn on a surface of a given genus. In this terminology, planar graphs have graph genus 0, since the plane (and the sphere) are surfaces of genus 0. See "graph embedding" for other related topics.

Contents

Kuratowski's and Wagner's theorems

The Polish mathematician Kazimierz Kuratowski provided a characterization of planar graphs in terms of forbidden graphs, now known as Kuratowski's theorem:

A finite graph is planar if and only if it does not contain a subgraph that is a subdivision of K5 (the complete graph on five vertices) or K3,3 (complete bipartite graph on six vertices, three of which connect to each of the other three).

A subdivision of a graph results from inserting vertices into edges (for example, changing an edge •——• to •—•—•) zero or more times. Equivalent formulations of this theorem, also known as "Theorem P" include

A finite graph is planar if and only if it does not contain a subgraph that is homeomorphic to K5 or K3,3.

In the Soviet Union, Kuratowski's theorem was known as the Pontryagin-Kuratowski theorem, as its proof was allegedly first given in Pontryagin's unpublished notes. By a long-standing academic tradition, such references are not taken into account in determining priority, so the Russian name of the theorem is not acknowledged internationally.

An example of a graph which doesn't have K5 or K3,3 as its subgraph. However, it has a subgraph that is homeomorphic to K3,3 and is therefore not planar.

Instead of considering subdivisions, Wagner's theorem deals with minors:

A finite graph is planar if and only if it does not have K5 or K3,3 as a minor.

Klaus Wagner asked more generally whether any minor-closed class of graphs is determined by a finite set of "forbidden minors". This is now the Robertson-Seymour theorem, proved in a long series of papers. In the language of this theorem, K5 and K3,3 are the forbidden children for the class of finite planar graphs.

Other planarity criteria

In practice, it is difficult to use Kuratowski's criterion to quickly decide whether a given graph is planar. However, there exist fast algorithms for this problem: for a graph with n vertices, it is possible to determine in time O(n) (linear time) whether the graph may be planar or not (see planarity testing).

For a simple, connected, planar graph with v vertices and e edges, the following simple planarity criteria hold:

Theorem 1. If v ≥ 3 then e ≤ 3v − 6;
Theorem 2. If v > 3 and there are no cycles of length 3, then e ≤ 2v − 4.

In this sense, planar graphs are sparse graphs, in that they have only O(v) edges, asymptotically smaller than the maximum O(v2). The graph K3,3, for example, has 6 vertices, 9 edges, and no cycles of length 3. Therefore, by Theorem 2, it cannot be planar. Note that these theorems provide necessary conditions for planarity that are not sufficient conditions, and therefore can only be used to prove a graph is not planar, not that it is planar. If both theorem 1 and 2 fail, other methods may be used.

For two planar graphs with v vertices, it is possible to determine in time O(v) whether they are isomorphic or not (see also graph isomorphism problem).[1]

Euler's formula

Euler's formula states that if a finite, connected, planar graph is drawn in the plane without any edge intersections, and v is the number of vertices, e is the number of edges and f is the number of faces (regions bounded by edges, including the outer, infinitely-large region), then

v − e + f = 2.

As an illustration, in the butterfly graph given above, v = 5, e = 6 and f = 3. If the second graph is redrawn without edge intersections, it has v = 4, e = 6 and f = 4. In general, if the property holds for all planar graphs of f faces, any change to the graph that creates an additional face while keeping the graph planar would keep v − e + f an invariant. Since the property holds for all graphs with f = 2, by mathematical induction it holds for all cases. Euler's formula can also be proven as follows: if the graph isn't a tree, then remove an edge which completes a cycle. This lowers both e and f by one, leaving v − e + f constant. Repeat until the remaining graph is a tree; trees have v =  e + 1 and f = 1, yielding v − e + f = 2. i.e. the Euler characteristic is 2.

In a finite, connected, simple, planar graph, any face (except possibly the outer one) is bounded by at least three edges and every edge touches at most two faces; using Euler's formula, one can then show that these graphs are sparse in the sense that e ≤ 3v − 6 if v ≥ 3.

The Goldner–Harary graph is maximal planar. All its faces are bounded by three edges.

A simple graph is called maximal planar if it is planar but adding any edge (on the given vertex set) would destroy that property. All faces (even the outer one) are then bounded by three edges, explaining the alternative terms triangular and triangulated for these graphs. If a triangular graph has v vertices with v > 2, then it has precisely 3v − 6 edges and 2v − 4 faces.

Euler's formula is also valid for simple polyhedra. This is no coincidence: every simple polyhedron can be turned into a connected, simple, planar graph by using the polyhedron's vertices as vertices of the graph and the polyhedron's edges as edges of the graph. The faces of the resulting planar graph then correspond to the faces of the polyhedron. For example, the second planar graph shown above corresponds to a tetrahedron. Not every connected, simple, planar graph belongs to a simple polyhedron in this fashion: the trees do not, for example. Steinitz's theorem says that the polyhedral graphs formed from convex polyhedra (equivalently: those formed from simple polyhedra) are precisely the finite 3-connected simple planar graphs.

Related families of graphs

Outerplanar graphs are graphs with an embedding in the plane such that all vertices belong to the unbounded face of the embedding. Every outerplanar graph is planar, but the converse is not true: K4 is planar but not outerplanar. A theorem similar to Kuratowski's states that a finite graph is outerplanar if and only if it does not contain a subdivision of K4 or of K2,3.

A 1-outerplanar embedding of a graph is the same as an outerplanar embedding. For k > 1 a planar embedding is k-outerplanar if removing the vertices on the outer face results in a (k − 1)-outerplanar embedding. A graph is k-outerplanar if it has a k-outerplanar embedding

An apex graph is a graph that may be made planar by the removal of one vertex, and a k-apex graph is a graph that may be made planar by the removal of at most k vertices.

A toroidal graph is a graph that can be embedded without crossings on the torus. More generally, the genus of a graph is the minimum genus of a two-dimensional graph onto which the graph may be embedded; planar graphs have genus zero and nonplanar toroidal graphs have genus one.

Any graph may be embedded into three-dimensional space without crossings. However, a three-dimensional analogue of the planar graphs is provided by the linklessly embeddable graphs, graphs that can be embedded into three-dimensional space in such a way that no two cycles are topologically linked with each other. In analogy to Kuratowski's and Wagner's characterizations of the planar graphs as being the graphs that do not contain K5 or K3,3 as a minor, the linklessly embeddable graphs may be characterized as the graphs that do not contain as a minor any of the seven graphs in the Petersen family. In analogy to the characterizations of the outerplanar and planar graphs as being the graphs with Colin de Verdière graph invariant at most two or three, the linklessly embeddable graphs are the graphs that have Colin de Verdière invariant at most four.

Other facts and definitions

Every planar graph without loops is 4-partite, or 4-colorable; this is the graph-theoretical formulation of the four color theorem.

Fáry's theorem states that every simple planar graph admits an embedding in the plane such that all edges are straight line segments which don't intersect. Similarly, every simple outerplanar graph admits an embedding in the plane such that all vertices lie on a fixed circle and all edges are straight line segments that lie inside the disk and don't intersect.

A planar graph and its dual

Given an embedding G of a (not necessarily simple) connected graph in the plane without edge intersections, we construct the dual graph G* as follows: we choose one vertex in each face of G (including the outer face) and for each edge e in G we introduce a new edge in G* connecting the two vertices in G* corresponding to the two faces in G that meet at e. Furthermore, this edge is drawn so that it crosses e exactly once and that no other edge of G or G* is intersected. Then G* is again the embedding of a (not necessarily simple) planar graph; it has as many edges as G, as many vertices as G has faces and as many faces as G has vertices. The term "dual" is justified by the fact that G** = G; here the equality is the equivalence of embeddings on the sphere. If G is the planar graph corresponding to a convex polyhedron, then G* is the planar graph corresponding to the dual polyhedron.

Duals are useful because many properties of the dual graph are related in simple ways to properties of the original graph, enabling results to be proven about graphs by examining their dual graphs.

While the dual constructed for a particular embedding is unique (up to isomorphism), graphs may have different (i.e. non-isomorphic) duals, obtained from different (i.e. non-homeomorphic) embeddings.

A Euclidean graph is a graph in which the vertices represent points in the plane, and the edges are assigned lengths equal to the Euclidean distance between those points; see Geometric graph theory.

A plane graph is said to be convex if all of its faces (including the outer face) are convex polygons. A planar graph may be drawn convexly if and only if it is a subdivision of a 3-vertex-connected planar graph.

The circle packing theorem states that the family of planar graphs coincides with the family of intersection graphs for the sets of closed disks in the plane which intersect only at boundary points. Similarly, Scheinerman's conjecture (now a theorem) states that every planar graph can also be represented as an intersection graph of line segments in the plane.

The planar separator theorem states that every n-vertex planar graph can be partitioned into two subgraphs of size at most 2n/3 by the removal of O(√n) vertices. As a consequence, planar graphs also have treewidth and branch-width O(√n).

Applications

Notes

  1. ↑ I. S. Filotti, Jack N. Mayer. A polynomial-time algorithm for determining the isomorphism of graphs of fixed genus. Proceedings of the 12th Annual ACM Symposium on Theory of Computing, p.236–243. 1980.
  2. ↑ Nick Pearson, Planar graphs and the Travelling Salesman Problem, Lancaster University, April 19th 2005

References

External links